Continua l’avventura per realizzare il catino absidale della Chiesa di San Antonio a San Benedetto del Tronto.
Dopo aver analizzato le formule pervenute dall’arch. Beniamino Tagliabue del politecnico di Milano
| R= | 500 | cm | (raggio sfera) | ||||||||||||||||||||||||||||||
| n= | 30 | (parti in cui è divisa l’ottava parte di sfera 90° x 90°) | |||||||||||||||||||||||||||||||
| 90° | 1,570796 | rad | |||||||||||||||||||||||||||||||
| k | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | |||
| r | 26,168 | 52,264 | 78,217 | 103,956 | 129,410 | 154,508 | 179,184 | 203,368 | 226,995 | 250,000 | 272,320 | 293,893 | 314,660 | 334,565 | 353,553 | 371,572 | 388,573 | 404,508 | 419,335 | 433,013 | 445,503 | 456,773 | 466,790 | 475,528 | 482,963 | 489,074 | 493,844 | 497,261 | 499,315 | 500,000 | cm | ||
| q | 0,052 | 0,105 | 0,157 | 0,209 | 0,262 | 0,314 | 0,367 | 0,419 | 0,471 | 0,524 | 0,576 | 0,628 | 0,681 | 0,733 | 0,785 | 0,838 | 0,890 | 0,942 | 0,995 | 1,047 | 1,100 | 1,152 | 1,204 | 1,257 | 1,309 | 1,361 | 1,414 | 1,466 | 1,518 | 1,571 | rad | ||
| s | 26,180 | 52,360 | 78,540 | 104,720 | 130,900 | 157,080 | 183,260 | 209,440 | 235,619 | 261,799 | 287,979 | 314,159 | 340,339 | 366,519 | 392,699 | 418,879 | 445,059 | 471,239 | 497,419 | 523,599 | 549,779 | 575,959 | 602,139 | 628,319 | 654,498 | 680,678 | 706,858 | 733,038 | 759,218 | 785,398 | cm | ||
| x | 0 | 26,171 | 52,342 | 78,513 | 104,684 | 130,856 | 157,028 | 183,200 | 209,372 | 235,545 | 261,718 | 287,891 | 314,065 | 340,240 | 366,414 | 392,590 | 418,766 | 444,943 | 471,120 | 497,298 | 523,476 | 549,655 | 575,835 | 602,015 | 628,195 | 654,376 | 680,558 | 706,740 | 732,923 | 759,106 | 785,289 | cm | |
| y | 0 | 0,685 | 1,368 | 2,047 | 2,721 | 3,388 | 4,045 | 4,690 | 5,324 | 5,942 | 6,544 | 7,128 | 7,693 | 8,237 | 8,758 | 9,255 | 9,727 | 10,172 | 10,589 | 10,977 | 11,335 | 11,662 | 11,957 | 12,219 | 12,448 | 12,642 | 12,802 | 12,927 | 13,017 | 13,071 | 13,088 | cm | |
| x, y coordinate della spezzata che delimita lo sviluppo in piano della parte di sfera) | |||||||||||||||||||||||||||||||||
optiamo per l’utilizzo di software per lo sviluppo della grafica dalla superficie a doppia curvatura al piano.
La scelta è quasi obbligata al programma giapponese Pepakura della Tamasoft.
Dopo la fase di stampa e taglio su un Roland VersaCamm SP-540 iniziamo a montare le fette sul campione in scala in polistirolo.
Oltre ai problemi in fase di montaggio, notiamo che il problema degli accostamenti delle strisce è evidenziato in base alla modifica anche lieve della superficie di applicazione.
Questo test blocca lo sviluppo. La soluzione finora perseguita, basata sulle strisce, non è fattibile!
La nuova soluzione è arrivata dall’analisi delle vetrate artistiche.
La suddivisione della grafica da applicare il elementi semplici che seguano le dinamiche della grafica stessa è la giusta soluzione.
L’utilizzo di elementi semplici e piccoli consente una deformazione senza alterazione.
Viene ricreato su Rhinoceros una cupola in elementi poligonali più fitti della precedente. Sul software Pepakura, dopo aver applicato la bitmap distorta iniziano gli aggiustamenti creando delle linee di taglio che seguono la dinamica della grafica.
Il risultato è un insieme di elementi da ricomporre e applicare nel nostro solito campione in polistirolo.
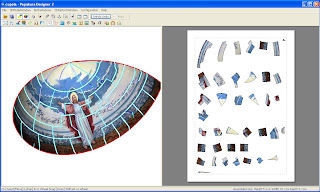Non siamo riusciti a creare la prima cupola in affresco digitale per l’inaugurazione della chiesa. Preferiamo concentrarci sullo sviluppo e sull’eccellenza della realizzazione anzichè presentare qualcosa di “bello” giusto per coprire una parete bianca.
Noi siamo per l’eccellenza e a volte per eccellere serve più tempo del dovuto.
….continua
